[科学网]东方随机过程

一直对贝叶斯理论和MCMC 过程理解不明了，在查资料的过程中，看到一个有趣的问题：

东方随机过程

大小姐蕾米最喜欢B型血。

女仆长咲夜每天一早会到野外搜集新鲜的血液。从每个人身上可以采集到一个单位的血液。咲夜每天采集到若干个人的血液后返回红魔馆。假设人群中B型血的概率为四分之一。

蕾米每天对B型血的需求量是随心情而定的。我们假设需求量服从均值为一的指数分布。

如果咲夜采集到的B型血不能满足蕾米的需求，咲夜会受到训斥。在受到训斥之后的一天，咲夜会多采集一个人的血液。如果某天B型血的消耗量不到采集量的一半，第二天咲夜会少采集一个人的血液。如果这两件事情都没有发生，第二天采集人数和前一天相同。

请问在长时间之下：

1. 咲夜平均每天要采集几个人的血液？
2. 咲夜受到训斥的天数占多少比例？”

心里也不知道用纯数学的方法该怎么解这个问题，不过学过一点点的编程知识，顺便就用R写了一个代码，把它解了出来，但是还是希望能有数学教好的朋友能帮忙给出纯数学上的解答。

根据已知条件可知: 蕾米对血的需求量服从均值为1的指数分布：我们假设10000天的血需求量为：

R 编写代码如下：
eat_blood <- rexp(10000,rate=1)
#初始采集血液的人数
N=6
#获得B型血量
B_blood <- N *1/4
#初始是否被骂:
sad <- F
#统计被骂次数
sadtimes <- 0
#统计10000天的采血人数
num_person <- NULL
#随机模型开始
for (i in 1:length(eat_blood)) {
#依据条件
　　if (B_blood < eat_blood[i]) {
　　　　N <- N+1
　　　　sad = T
　　　　sadtimes <- sadtimes +1
　　}
　　else {
　　　　if (eat_blood[i] < 1/2 * B_blood) {
　　　　　　N <- N-1
　　　　　　sad=F
　　　　}
　　　　else {
　　　　　　sad =F
　　　　}
　　}
　　B_blood <- 1/4*N
　　num_person <- c(num_person,N)
}
print(sadtimes/length(eat_blood))
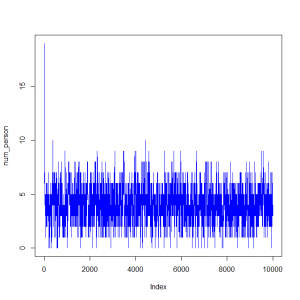
plot(num_person,type='l',col=blue)

10000次随机过程所采集血的人图示
#采血人数的期望值
summary(num_person)
N=4.088
#被责骂的比例
print(sadtimes/length(eat_blood))
#0.386

转自：http://blog.sciencenet.cn/blog-846085-651473.html