「十月随想祭」
先来看一个简单的物理问题,虽然这个问题应该是在高中发现的,但是其难度(本来)应该只有初中水平:
已知一质点的位移满足方程:s=2t+t^2,t是时间,求其速度。
按照:v=s/t,我们直接把上式两边全部除以一个t,就得到了速度的表达式:v=s/t=2+t,老师给这种做法判的是对。
可是,如果我们按照匀加速直线运动的位移公式:s=v’t+1/2at^2(这里的v‘是初速度)来对比题设方程的话,我们就可以认为,v'=2,1/2a=1(两多项式相等,对应系数相等),也就是v'=2,a=2,按照v=v'+at(也是匀加速运动的公式)则v=2+2t,与前者方法答案不符(老师判的错),何解?
当时对此一筹莫展,最近碰巧又想起了这个问题,于是又思考了一下,终于有了一个答案:我错了、老师也错了。
事实上,计算速度的通用公式是v=ds/dt,也就是位移s对时间t求导。故v=d(2t+t^2)/dt=2+2t,也就是第二个答案是正确的。那么第一个答案错在哪?v=s/t这个公式,若想让v表示瞬时速度,是只能适用于匀速运动,显然这里是变速运动,所以v=s/t在这里并不适用。其v的物理含义是“平均速度”而非“速度”。所以v=2+t的真正含义是“平均速度与时间的函数关系”。
好了,正片开始:
大家肯定知道这么个东西:
按照:v=s/t,我们直接把上式两边全部除以一个t,就得到了速度的表达式:v=s/t=2+t,老师给这种做法判的是对。
可是,如果我们按照匀加速直线运动的位移公式:s=v’t+1/2at^2(这里的v‘是初速度)来对比题设方程的话,我们就可以认为,v'=2,1/2a=1(两多项式相等,对应系数相等),也就是v'=2,a=2,按照v=v'+at(也是匀加速运动的公式)则v=2+2t,与前者方法答案不符(老师判的错),何解?
当时对此一筹莫展,最近碰巧又想起了这个问题,于是又思考了一下,终于有了一个答案:我错了、老师也错了。
事实上,计算速度的通用公式是v=ds/dt,也就是位移s对时间t求导。故v=d(2t+t^2)/dt=2+2t,也就是第二个答案是正确的。那么第一个答案错在哪?v=s/t这个公式,若想让v表示瞬时速度,是只能适用于匀速运动,显然这里是变速运动,所以v=s/t在这里并不适用。其v的物理含义是“平均速度”而非“速度”。所以v=2+t的真正含义是“平均速度与时间的函数关系”。
好了,正片开始:
大家肯定知道这么个东西:
中学物理老师一般通过这个道具来演示动量守恒。注意,中间两个小球是没有移动的,我们把它们固定在那也不会影响左边的小球被弹飞。也就是说我们把中间俩小球换成一个圆柱体是不影响实验结果的:

只要小球和圆柱是刚体,产生的是弹性碰撞,下面的小球就会按照动量守恒原则以相同速度被弹出。而需要注意一点的是,这里圆柱是否固定是不影响实验结果的,因为就算固定了,也不会存在外力——注意,动量守恒的一个条件就是没有外力影响。
那么我们假如继续抽象一下实验物体,把小球想象成一个粒子,圆柱细成一个长条,然后(好戏开始了!)扭一下:
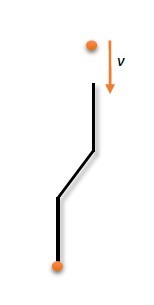
我们不考虑长条是不固定的情况,因为很复杂(这涉及动量和角动量的守恒),我们也不需要。我们继续把长条固定,这时如果再上面的粒子再碰撞长条,就会有外力参与这个过程了,粒子撞击长条,动量转换为冲量,其冲力在长条上传导,由于长条固定,所有垂直长条的力被抵消。那么最后下面的粒子受到的冲力就不等于原来上面粒子给长条的冲力了(F‘=cos^2(a),a是中间弯折的角度,显然,如果是90度弯折下面粒子就不会受力,上面小球就会被反弹了),动量也就不守恒了(因为有外力)。
但是如果这个长条是光滑的呢?(光滑的数学定义是光滑段上的所有点都存在n阶导数)
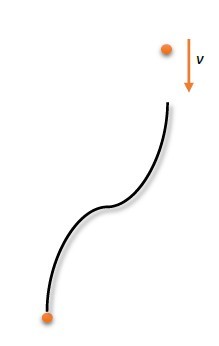
这个过程需要的数学比较高端,我现在还没有完成,不过我似乎已经完成了对一种比较特殊的分析:
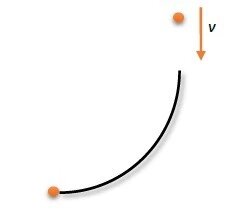
这种圆弧状的光滑长条如果被固定,那么下面那个粒子受到的力将不会有损耗。即F’=F,(这种情形的计算用高数知识就可以解决:涉及一个极限:lim(n→∞)[cos(a/n)]^2=1,a是任意正实数,所以说理论上这个圆弧就算是720°也没问题……实际没试过,不过猜想这样的话能量传播的损耗会比较大而使结果失准。)
其实我们可以做实验来验证一下,不过最近资金较紧……=。=(其实这种实验花不了多少钱,一般人是可以做的,等天时地利人和了就来做做好了~=w=)
于是我的猜想其实是:只要这个长条是光滑的,那么动量就不会有损失。(一般性证明正在努力中)
那,有人就会会问了:我说这些问题是要为什么? 我的回答必须是:还世界以本源~(^_^)v
那么,大家把这俩粒子想象成电子、想象成穿梭在某种固体中的自由电子(注意,并不是只有金属才有自由电子,是金属的自由电子比较多)。当然了,微观有着很多不同于宏观经典力学的特性,比如波粒二象性、量子化等等,我们暂时不去考虑这些影响我们思考的复杂限制。
首先,对于晶体,所有分子都会以自己的平衡位置做简谐振动。 自由电子想在其中穿行的话无法避免地会撞上那些分子或者其他的自由电子,所以对于这些自由电子有一个平均自由程的说法(气体分子也有这么一说)。拿导体为例,这种平均自由程宏观上也就体现为“电阻”。那么我们有什么办法让自由电子们的平均自由程按我们想的延长——比如无限长——对了,我想说的其实是超导问题,更进一步地,是“室温超导”。
大家都知道,一个静止的带电粒子周围存在电场,可以用E=kq/(r^2)来描述(其实我们更多地写成E=q/(4πε·r^2)),所以等势面是一个圆形,所以某种晶体中可能有这么一个情况:
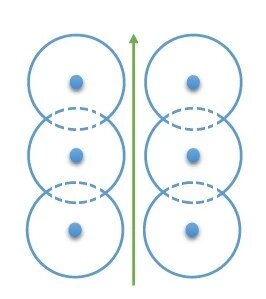
蓝色圆圈内代表自由电子无法进入的区域,绿色线条代表自由电子一个可能的运动轨道。当然了,这些分子还会不断振动,导致这条原本边界就不光滑的绿色通道更加曲折。有时还会暂时被封堵。
所以我们的目标很明显了,找到一种晶体结构,可以给自由电子提供光滑边界绿色边界的绿色通道——且是在一个比较高温度的状态。其实这种绿色通道和超导理论中的“量子隧道”几乎相同,不过要完成超导,还必须控制电子“流量”(Cooper电子对)等等。同时必须的,这些都预示着很多繁杂的计算(别忘了还有波粒二象性和量子化的限制!那些数学方程解起来可不是闹着玩的),关于我们想要的晶体结构我其实已经有一个定性的设想了,这里先卖个关子,因为在说这个之前我还有很多数学工作需要完成……
碎碎念:
“热血而不失理性”“不卑不亢”“不温不火”“执念太深”是我听到的对我几个比较中肯的评价。其实我对自己现在的人格是很满意的,虽然明显有些片面与问题存在,但是我认为这是我“保持自我”所必须付出的代价——我也愿意付出。现在我也越来越感受到,有些东西是需要用一生去证明的,而且在证明前别想别人会认可你,所谓“盖棺论定”大概和这个差不多意思吧?我的人生也差不多开始了,Can I?
只要小球和圆柱是刚体,产生的是弹性碰撞,下面的小球就会按照动量守恒原则以相同速度被弹出。而需要注意一点的是,这里圆柱是否固定是不影响实验结果的,因为就算固定了,也不会存在外力——注意,动量守恒的一个条件就是没有外力影响。
那么我们假如继续抽象一下实验物体,把小球想象成一个粒子,圆柱细成一个长条,然后(好戏开始了!)扭一下:
我们不考虑长条是不固定的情况,因为很复杂(这涉及动量和角动量的守恒),我们也不需要。我们继续把长条固定,这时如果再上面的粒子再碰撞长条,就会有外力参与这个过程了,粒子撞击长条,动量转换为冲量,其冲力在长条上传导,由于长条固定,所有垂直长条的力被抵消。那么最后下面的粒子受到的冲力就不等于原来上面粒子给长条的冲力了(F‘=cos^2(a),a是中间弯折的角度,显然,如果是90度弯折下面粒子就不会受力,上面小球就会被反弹了),动量也就不守恒了(因为有外力)。
但是如果这个长条是光滑的呢?(光滑的数学定义是光滑段上的所有点都存在n阶导数)
这个过程需要的数学比较高端,我现在还没有完成,不过我似乎已经完成了对一种比较特殊的分析:
这种圆弧状的光滑长条如果被固定,那么下面那个粒子受到的力将不会有损耗。即F’=F,(这种情形的计算用高数知识就可以解决:涉及一个极限:lim(n→∞)[cos(a/n)]^2=1,a是任意正实数,所以说理论上这个圆弧就算是720°也没问题……实际没试过,不过猜想这样的话能量传播的损耗会比较大而使结果失准。)
其实我们可以做实验来验证一下,不过最近资金较紧……=。=(其实这种实验花不了多少钱,一般人是可以做的,等天时地利人和了就来做做好了~=w=)
于是我的猜想其实是:只要这个长条是光滑的,那么动量就不会有损失。(一般性证明正在努力中)
那,有人就会会问了:我说这些问题是要为什么? 我的回答必须是:还世界以本源~(^_^)v
那么,大家把这俩粒子想象成电子、想象成穿梭在某种固体中的自由电子(注意,并不是只有金属才有自由电子,是金属的自由电子比较多)。当然了,微观有着很多不同于宏观经典力学的特性,比如波粒二象性、量子化等等,我们暂时不去考虑这些影响我们思考的复杂限制。
首先,对于晶体,所有分子都会以自己的平衡位置做简谐振动。 自由电子想在其中穿行的话无法避免地会撞上那些分子或者其他的自由电子,所以对于这些自由电子有一个平均自由程的说法(气体分子也有这么一说)。拿导体为例,这种平均自由程宏观上也就体现为“电阻”。那么我们有什么办法让自由电子们的平均自由程按我们想的延长——比如无限长——对了,我想说的其实是超导问题,更进一步地,是“室温超导”。
大家都知道,一个静止的带电粒子周围存在电场,可以用E=kq/(r^2)来描述(其实我们更多地写成E=q/(4πε·r^2)),所以等势面是一个圆形,所以某种晶体中可能有这么一个情况:
蓝色圆圈内代表自由电子无法进入的区域,绿色线条代表自由电子一个可能的运动轨道。当然了,这些分子还会不断振动,导致这条原本边界就不光滑的绿色通道更加曲折。有时还会暂时被封堵。
所以我们的目标很明显了,找到一种晶体结构,可以给自由电子提供光滑边界绿色边界的绿色通道——且是在一个比较高温度的状态。其实这种绿色通道和超导理论中的“量子隧道”几乎相同,不过要完成超导,还必须控制电子“流量”(Cooper电子对)等等。同时必须的,这些都预示着很多繁杂的计算(别忘了还有波粒二象性和量子化的限制!那些数学方程解起来可不是闹着玩的),关于我们想要的晶体结构我其实已经有一个定性的设想了,这里先卖个关子,因为在说这个之前我还有很多数学工作需要完成……
碎碎念:
“热血而不失理性”“不卑不亢”“不温不火”“执念太深”是我听到的对我几个比较中肯的评价。其实我对自己现在的人格是很满意的,虽然明显有些片面与问题存在,但是我认为这是我“保持自我”所必须付出的代价——我也愿意付出。现在我也越来越感受到,有些东西是需要用一生去证明的,而且在证明前别想别人会认可你,所谓“盖棺论定”大概和这个差不多意思吧?我的人生也差不多开始了,Can I?
本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可。
