数字虚空\/Digital Void 编写手记:整体结构与正交投影
这学期三门编程语言课,目测是每门课都会要求有大作业式的编程作业。C#的大作业原本留的是什么日记本,可是我看着这个题目就提不起劲,之前数据结构课设的时候就已经用MFC写过通讯录了,而C#可是比MFC还容易的……于是我就去问老师能不能换题目,并拿了之前MFC以及大数计算(C++课设)举例,老师的态度很明确:作业的考核的目标是你对C#各种可视化控件的使用,而非数据结构或算法,选题可以自选,但是不能偏离这个中心。于是我就跑图书馆去找了一下相关的书籍,本来我想做个3D游戏,可是一查发现C#的3D基本是基于DX或者XNA类库的,而如果使用这些类库,C#本身也会退居二线(对于类库的使用则是主要),这样必然也是不符合要求的。不过我发现了这么一本书《C#二维三维图形绘制工程实例》,里面基本是用GDI+做了几个类似MATLAB的函数图像窗口。我马上想到了我之前就在想的一个东西,之前接触《三体》的时候就见过三体运动的模拟软件,不过大多都是2D的,我于是就准备做一个3D的。名字也是很快就有了主意:数字虚空。其实我对这个东西的期望不仅是模拟天体运动,不过这是后话了,先把这个一期目标完成吧。
而且除了对原题目难度的不满这个原因外,缺少数学则是另外一个重要的原因。缺少数学的编程就真的和程序猿无异。至少在这几天的编写过程中,我有几乎一半的时间都是在解决各种数学问题。至少对于我自己,我不会觉得自己是一个程序猿,而像一个工程师,在建造一个我感兴趣,我需要的实验大棚。若编程仅仅是为娱乐,而忘记了科学研究这个计算机的原始目的……那我就不奉陪了。
下图就是一个模拟双星系统的GIF图,我大约就是要做它的三维版:

首先是整个系统的结构,乍看之下确实有点复杂,不过也就那么回事,以后可能还会修改倒是了,因为这些图不仅要拿出来给各位看,我自己有时也要参考(就像大棚的设计图纸嘛),所以就稍微用了点心画漂亮了点=w=:
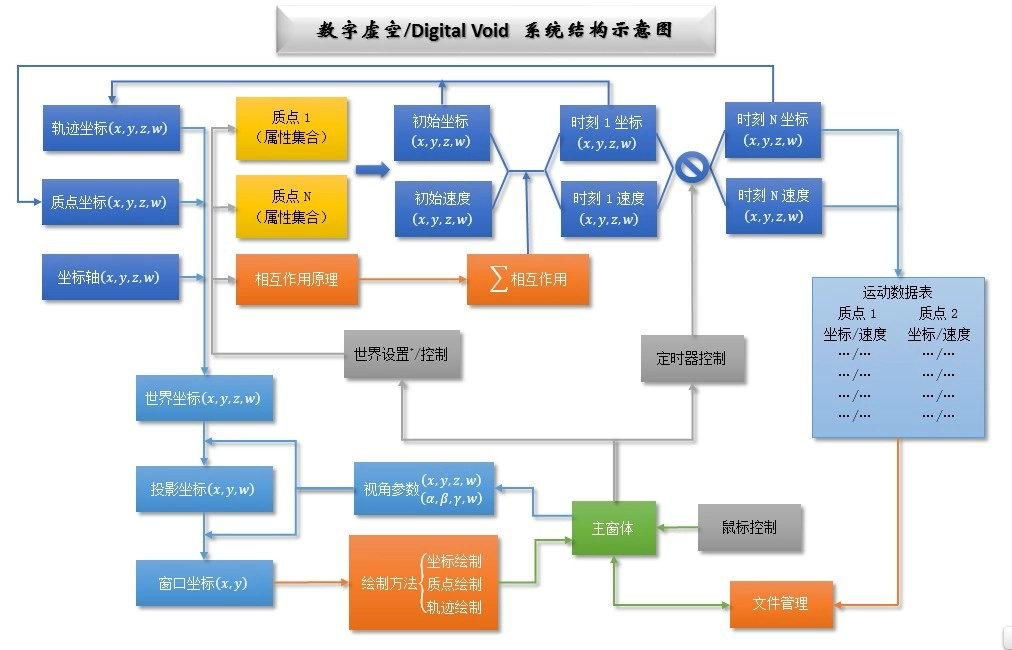
首先,世界坐标和投影坐标是采用的齐次坐标(x,y,z,w)的形式,这种坐标书上说是方便平移变换,不过我在实际编程过程中发现那个第四维w确实大有用武之地:一般来说w=1,w=0时这个点就是无穷远点,程序里我也靠这个来判断这个点是否需要处理(显示)。
接下来我首先完成的是世界坐标→窗口坐标的部分,这里就涉及到正交投影的问题,我没使用透视投影,一方面透视投影更为复杂,另一方面也更难控制——而这会降低用户体验。其实第二点是主要原因,现在看来要把正交投影改为透视投影程序上并不困难。
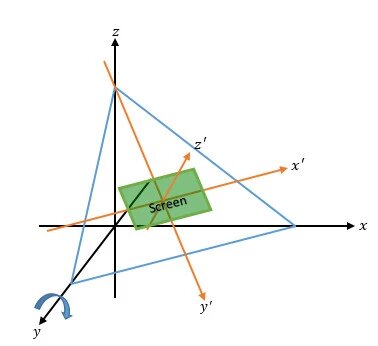
如上图,世界坐标系x,y,z首先变换成投影坐标系x',y',z',然后变换为窗口坐标x,y。世界坐标变换成投影坐标的变换过程我参考的维基百科“三维投影”:
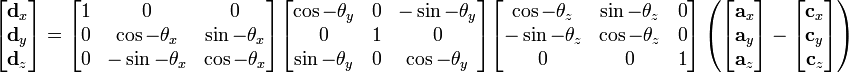
其中,dx,dy,dz是物体的投影坐标,ax,ay,az是物体的世界坐标,c和θ是投影坐标系的世界坐标位置和视野角度矢量。
而这只是基本的点的正交投影,直线呢?这个问题的引入是因为,我想做坐标轴的投影。进一步地,我们在坐标轴(直线)上随意选择两个不同的点, 对这两个点进行正交投影,得到他们的投影坐标——这个坐标可能落在显示屏幕内,也可能在外面。于是问题是,我们怎么判断这两个点所在的直线是否穿过屏幕矩形?如果穿过,我需要它与矩形的交点坐标,这样我才能把这条直线表示出来。
我们把这个数学问题重述一遍:已知两个点的坐标(x1,y1)(x2,y2),其所在的直线若穿过矩形(0<x<a,0<y<b) ,给出交点坐标。
这个问题本来对于人来说非常简单,但是让计算机来做就有点麻烦——我为此想了两天Orz……如果就是按着if else来写的话实在需要太多的判断。我不喜欢这样,现在我是这么一个方法:
1.判断特殊情况,即与坐标轴平行的情况(3种情况,与x轴平行,与y轴平行,两点为一点)
2.直线存在两点式时,分别判断与矩形各边的相交情况(4次判断) ,新建一个点类的数组,如果出现相交情况,就把交点存入数组,同时数组指针+1.
3.无交点时,数组第一个点的x坐标值赋-1,程序靠这个来判断是否存在交点。
存在交点时最多也只可能有两个交点,相当于利用4个判断和一个数组完成了对6种情况的分析。不知道这算不算一个策(suan)略(fa)……=。= 各位有啥更好的想法欢迎和我交流啊~~
下一步是完成鼠标控制,本来我还有想曲线的投影问题的——我还想把质点做成球体的外观,不过暂时还没啥好想法。这个问题就先放着吧,不行就去掉好了…………
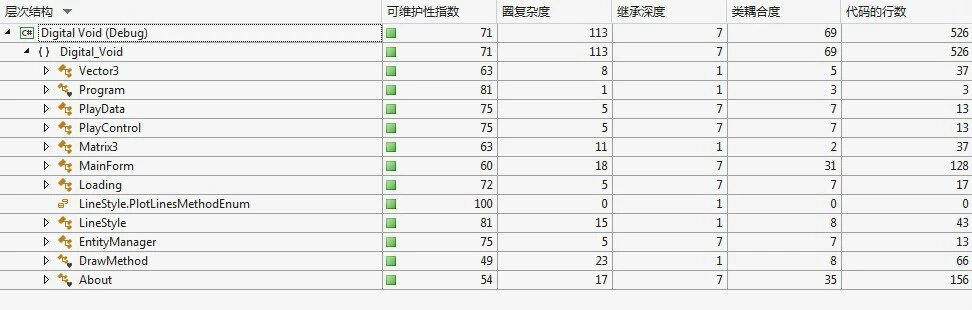
主界面暂时还没啥好看的,贴一张VS2013的代码度量值吧,以下是目前的进度(PlayData,PlayControl,Loading,EntityManager,About都还是壳子,DrawMethod只写了坐标轴的绘制方法……Orz)
而且除了对原题目难度的不满这个原因外,缺少数学则是另外一个重要的原因。缺少数学的编程就真的和程序猿无异。至少在这几天的编写过程中,我有几乎一半的时间都是在解决各种数学问题。至少对于我自己,我不会觉得自己是一个程序猿,而像一个工程师,在建造一个我感兴趣,我需要的实验大棚。若编程仅仅是为娱乐,而忘记了科学研究这个计算机的原始目的……那我就不奉陪了。
下图就是一个模拟双星系统的GIF图,我大约就是要做它的三维版:
首先是整个系统的结构,乍看之下确实有点复杂,不过也就那么回事,以后可能还会修改倒是了,因为这些图不仅要拿出来给各位看,我自己有时也要参考(就像大棚的设计图纸嘛),所以就稍微用了点心画漂亮了点=w=:

首先,世界坐标和投影坐标是采用的齐次坐标(x,y,z,w)的形式,这种坐标书上说是方便平移变换,不过我在实际编程过程中发现那个第四维w确实大有用武之地:一般来说w=1,w=0时这个点就是无穷远点,程序里我也靠这个来判断这个点是否需要处理(显示)。
接下来我首先完成的是世界坐标→窗口坐标的部分,这里就涉及到正交投影的问题,我没使用透视投影,一方面透视投影更为复杂,另一方面也更难控制——而这会降低用户体验。其实第二点是主要原因,现在看来要把正交投影改为透视投影程序上并不困难。
如上图,世界坐标系x,y,z首先变换成投影坐标系x',y',z',然后变换为窗口坐标x,y。世界坐标变换成投影坐标的变换过程我参考的维基百科“三维投影”:
其中,dx,dy,dz是物体的投影坐标,ax,ay,az是物体的世界坐标,c和θ是投影坐标系的世界坐标位置和视野角度矢量。
而这只是基本的点的正交投影,直线呢?这个问题的引入是因为,我想做坐标轴的投影。进一步地,我们在坐标轴(直线)上随意选择两个不同的点, 对这两个点进行正交投影,得到他们的投影坐标——这个坐标可能落在显示屏幕内,也可能在外面。于是问题是,我们怎么判断这两个点所在的直线是否穿过屏幕矩形?如果穿过,我需要它与矩形的交点坐标,这样我才能把这条直线表示出来。
我们把这个数学问题重述一遍:已知两个点的坐标(x1,y1)(x2,y2),其所在的直线若穿过矩形(0<x<a,0<y<b) ,给出交点坐标。
这个问题本来对于人来说非常简单,但是让计算机来做就有点麻烦——我为此想了两天Orz……如果就是按着if else来写的话实在需要太多的判断。我不喜欢这样,现在我是这么一个方法:
1.判断特殊情况,即与坐标轴平行的情况(3种情况,与x轴平行,与y轴平行,两点为一点)
2.直线存在两点式时,分别判断与矩形各边的相交情况(4次判断) ,新建一个点类的数组,如果出现相交情况,就把交点存入数组,同时数组指针+1.
3.无交点时,数组第一个点的x坐标值赋-1,程序靠这个来判断是否存在交点。
存在交点时最多也只可能有两个交点,相当于利用4个判断和一个数组完成了对6种情况的分析。不知道这算不算一个策(suan)略(fa)……=。= 各位有啥更好的想法欢迎和我交流啊~~
下一步是完成鼠标控制,本来我还有想曲线的投影问题的——我还想把质点做成球体的外观,不过暂时还没啥好想法。这个问题就先放着吧,不行就去掉好了…………
主界面暂时还没啥好看的,贴一张VS2013的代码度量值吧,以下是目前的进度(PlayData,PlayControl,Loading,EntityManager,About都还是壳子,DrawMethod只写了坐标轴的绘制方法……Orz)
本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可。
